Philip Liebson
Chicago, Illinois, United States
 |
| Euclid Ptolemy |
The Alexandrian tradition was first manifested in the Royal Museum in Alexandria, established by the Ptolomies who ruled over Egypt at that time. The museum contained the royal library, one of the largest and most significant resources of the ancient world. Established in the third century BC, it functioned as a major center until Egypt was conquered by the Romans in 30 BC. It contained collections of works, lecture halls, meeting rooms, and gardens. The library was part of a larger research institution called the museum, which contained the work of Aristotle’s Lyceum among others. It should be noted that the word museum was derived from this structure, dedicated to the muses. Besides the enormous library, the museum had lecture halls, zoos, menageries, observation stations, and living rooms. The Egyptian government played a larger role in scientific research than that of the Greeks. Precision, exactitude, and empiricism were found here instead of the induction and generality of the Greeks.
The Alexandrian period, between the third century and the last few decades at the end of the first century BC provided advances in mathematics and science, especially astronomy, optics, and mechanics, that encompassed not only Alexandria itself, but educated notable Greek mathematicians and scientists (Archimedes and Apollonius among them) who studied in the School of Euclid in Alexandria.
Perhaps the first great scholar that Alexandria produced was Euclid (365-285 BC). He was most important in the field of mathematics. He was characteristic of the period in his systematization of knowledge, doing little original thinking but bringing together Greek concepts of mathematics and correlating them. Scientifically he is attached to the Platonic philosophy. He made the goal of his Elements the construction of five regular polygons of Plato.
 |
| The Library of Alexandria |
Euclid’s treatise has served as the basis for all elementary geometrical instruction up to the present day. In the Elements he emphasizes synthesis, although in other works he depends on analysis as well. He developed the six-stage method of proving a theorem. which is still being taught today. This methodology involves enunciation (the statement of the theorem in general terms), setting out (the restatement of the theorem in particular terms, such as the use of a geometrical figure), specification (the relation of the enunciation to the diagram), construction (the arbitrary use of auxiliary lines), proof (which involves axioms, definitions, and previously proved theorems) and finally the restatement of the enunciation (at the end of the proof).
There is a careful avoidance of whatever is not geometrical and no attempt is made to develop initiative or invention on the part of the student. In Euclid’s mathematical system are found postulates, definitions, common notations and rules of inference that constitute its framework. Euclid characterizes the Greek avoidance of infinities by careful definition and limitation, so as to exclude infinity not immediately apparent to the senses. Euclid based his definitions on elements that were “apparent,” characterized by the “setting out” of his theorems. Thus we find here a leaning toward geometrical intuition, found in such axioms as “the whole being greater than any of its parts.”
In recent times, the question has arisen whether the basic axioms of Euclid need be accepted. It is felt that they are not necessities of thought and that quite different axioms can be postulated and a perfectly self-consistent system of geometry built up from them. This is the case with the non-Euclidean system of Riemann for example. In that period,however, it was probably inconceivable that a universe could be finite in space, the space itself still being considered unlimited. Possibly, with the avoidance of infinities prevalent at the time, it would be extremely interesting to see how the Euclideans would have reacted to the theoretical Klein bottle or Mobius strip, concepts of three or two dimensional infinities respectively. For Euclid, they could not exist because they could not be defined.
 |
| The five platonic solids |
Besides the Elements, Euclid wrote treatises on Fallacies, designed to safeguard the student from erroneous reasoning, on conic sections, and ion the applications of geometry, as found in the Phenomena, Optics, and Catoptrics. The Phenomena is a treatise on the traditional spherics with special reference to elementary astronomy. The work is purely geometrical and there was no attempt to formulate a system of planetary, lunar, or solar motions. His Optics is a study of light rays. He believed that rays of light come from the eye in a cone of vision. Catoptrics concerns the mathematical theory of mirrors, particularly the images formed in plane and spherical concave mirrors. Perspective is also dealt with in this work. Examples of several propositions found in the work are: equal magnitudes situated at different distances from the eye appear unequal, and the nearer always appear larger; parallel lines when seen from a distance appear to be an unequal distance apart. We see that he is basing his propositions of apparent phenomena that can be seen and felt geometrically. If it is felt to be “right” geometrically, then it probably can be proven. Thus, these propositions do not depend here on absolute properties of geometric figures, but relative ones.
The second great name in the Alexandrian period and one of the greatest in the history of science is that of Archimedes (c.287-c.212 BC). He was not strictly speaking of the Alexandrian school (although he studied in Alexandria under the followers of Euclid) but was born and spent most of his life in Syracuse, which was at that time a Greek seaport. He was a geometer, mathematician, and engineer. He enriched Euclidean geometry, made important progress in algebra, laid the foundations of mechanics, and anticipated calculus. With the latter we come to the problem of infinitesimals again. In “The Method,” Archimedes showed the use of notions of infinitesimals as means of discovery. He used geometric construction to analyze areas under curves, by dividing the areas into smaller and smaller strips and summing up the total of these small areas, anticipating integral calculus. He dealt in this way with volumes within complex curves. He was still cautious, however, about discussing infinitesimals between the lines, in plane figures, or between planes, in solids, even though his method involved such a concept. This reflects the wariness of the mathematicians of the time towards discussing the infinitesimal and had been found in the criticisms of Zeno (cf. III- The Science of Greece). Archimedes was more original in his mathematical papers than Euclid. Among some of his achievements in mathematics is the calculation of the ratio of the circumference of a circle to its diameter, important advances in measurements of the circle in general and in the geometry of spheres and cylinders. Archimedes achieved a more developed sense of numerical computation than Euclid, who discussed proportionalities without regard to an actual proportionality factor. Archimedes had a far-ranging interest in applications; for example, discovering the principles of hydrostatics and inventing several war machines to protect his native Syracuse from invasion.
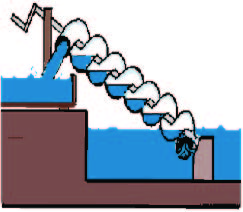 |
| The Archimedes screw for pumping water |
He is also credited with designing innovative machines, such as his screw pump, compound pulley, catapult, and other machines of war. This was unlike Euclid, who shared the views of certain old philosophical traditions that the practical applications of a science involve little constructive thought and is therefore unworthy. He treated the lever and the wedge mathematically, setting out laws of equilibrium for bodies weighed on a balance, and dealt with the problem of determining centers of gravity of a variety of plane figures. He described an original apparatus for determining the angular diameter of the sun, evaluating its degree of accuracy. A notable comment attributed to him was that if he were given a lever long enough and a fulcrum on which to place it, he could move the world.
In other branches of mathematical science, Archimedes did even more important work, such as the algebra of linear equations. He showed mastery of the square root and comparison of irrational numbers with fractions. He also developed a notation comparable to the exponent for expressing large numbers. Other mathematical achievements include deriving an accurate approximation of pi and defining and investigating the spiral bearing his name. Perhaps the most practical discovery of Archimedes (the Archimedes principle) was that any object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.Of a more practical nature, he developed a screw for pumping water.
Apollonius of Perga (260-190 BC) was the last of the triumvirate of Alexandrian associated mathematicians who achieved fame. Although Greek, Apollonius studied in Alexandria under the pupils of Euclid and subsequently taught at the university there. He was known by his contemporaries as “The Great Geometer” and contributed work on conic sections. Euclid and Archimedes had experimented on passing different planes through right circular cones and had obtained ellipses, parabola and hyperbolae and which he had given them these names. He demonstrated that the basic conic property can be expressed in the same form with reference to any new diameter and the tangent at its extremity. Apollonius in the Conics further developed a method so similar to analytic geometry that his work is sometimes thought to have anticipated the work of Descartes by some 1800 years. He further developed relations between the abscissas and the corresponding ordinates that are equivalent to rhetorical equations of curves. Apollonius’s advances in mathematics came from working on the same problems that caused many mathematicians of the time to do original work, that of the duplication of the cube, squaring of the circle, and trisection of an angle. In astronomy, he developed the hypothesis of eccentric orbits, or epicycles, to explain the apparent motion of the planets and the varying speed of the Moon.
The great triumphs of Greek mathematics were predominantly in geometry, and the advances in the theory of numbers and arithmetic were made in close connection with geometry. Centuries after Archimedes and Apollonius, another Greek Alexandrian furthered mathematical theory. Diophantus (c. AD 210-290) was called the father of algebra. He wrote works on arithmetic: polynomials, and porisms, or miscellaneous propositions. An outstanding feature of Diophantus’s work is the use of symbols for the unknown and its powers and for subtraction. He did not deal with surds, imaginary roots, or negative solutions but confined himself only to positive rational solutions, integral or fractional. For his solution of a mixed quadratic equation he developed a formula similar to the modern quadratic formula based on completing the square. The work of Diophantus was studied by Greek and Arab mathematicians during the medieval period and it was approached with renewed interest during the Renaissance.
Besides mathematics, the Alexandrians interested themselves in other scientific pursuits and greatly developed the physical sciences of optics and mechanics. Optics had been studied in Greece under three headings, optics proper, which included perspective and vision, catoptrics, which encompassed reflection, images and mirrors, and synography, which was concerned with scenery making for theaters and other practical applications of optics. In addition, there was a side branch of optics named dioptrics, or refraction. The “visual ray” concept, previously described in the section on Euclid above, was derived from the Greeks as well as geometric optics. It was for the Alexandrians to discover important mathematical laws about reflection and refraction. Euclid, as mentioned previously, studied perspective and believed that rays of light came from the eye itself to the object seen in a “cone of vision.”
 |
| The sunbeams shown as two rays hitting the ground at Syene and Alexandria. Angle of sunbeam and the gnomons (vertical sticks) is shown at Alexandria, which allowed Eratosthenes’ estimates of radius and circumference of Earth |
Hero of Alexandria (c. AD10-70), whose main work was in the practical applications of mechanics, did some work in the field of optics, especially dealing with mirrors and reflection. He proved that the angle of incidence of a light ray stroking a mirror is equal to the angle of reflection. He also disputed Euclid’s hypothesis of a cone of vision, believing that light rays travel in a straight line from the eye, although still perceived as initiated from the eye. More importantly, he believed that light had an indefinitely great velocity. His efforts included the development of scientific instruments of practical utility, in addition to his study of the inclined plane.
Cleomedes, who lived sometime between the first century BC and the second century AD (most likely the first century BC) also considered the subject of the refraction of light. He explained many meteorological phenomena by the bending of light rays when they go through media of different densities. Claudius Ptolemy (c.AD 100-170) was another Greek living in Alexandria during the Roman period and was noted for his work on astronomy, astrology, and geography. He also contributed studies of light rays, considering the problem of rays passing from a medium of lower density to higher density, and discovered that in this case, the light ray bends toward the “normal” perpendicular to the surface of the denser medium. He measured the angles of refraction for various angles of incidence and developed an algebraic formula for refraction. Since Ptolemy had no knowledge of trigonometry, he could not develop a formula for finding refraction indices.
In the Alexandrian period, the areas of statics, hydrostatics, pneumatics, and dynamics were advanced significantly. Among the Alexandrians, we find the first person of note in the field of mechanics to be Strato, who lived in the third century BC. He may have entered the Aristotelean lyceum. He moved to Alexandria where he helped found the Museum and was a tutor to the King of Egypt. He made many experiments in pneumatics. He wanted to prove that air was corporeal. By inverting a bowl in a large vessel of water and seeing that the water would rise in the bowl but not too much, he adequately demonstrated that air was compressible, therefore corporeal, the space between the corpuscles being a vacuum. He believed that vacuums could exist naturally in a continuous condition, but did not believe there was an empty space, or vacuum, in the heavens. These ideas were influenced by the works of Democritus and Aristotle. He was opposed, however, to Aristotle’s belief that two of the four elements tended to move upward and two downward, believing that all four were influenced by gravity.
Alexandrians were concerned with the boundaries of the world around them. Geography had developed as a Greek tradition with the characterizations of broad regions by Homer in the Iliad and the Odyssey. It was believed that the world was surrounded by an ocean. It was generally accepted among the Greeks that the Earth was a sphere. Aristotle, in his work on meteorology had proved the shape of the Earth by seeing the shadow of the Earth in the Moon during a lunar eclipse. He set the diameter of the earth at 400,000 stadia (>45,000 miles), which was too large an estimate (Stadion=600 feet).Geography was important for the Alexandrians because of their extensive trade. In the third century BC, Eratosthenes, the chief librarian of the Alexandrian library, determined the latitudes of places on Earth using the gnomon, the part of a sundial that casts a shadow. He created the first map of the world incorporating parallels and meridians, based on the available geographical knowledge of the era. He also calculated the circumference of the Earth and its diameter using stadia, but his measurements were more accurate than that of Aristotle. He also calculated the distance from the Earth to the Sun with reasonable accuracy. Further, he provided measurements of chronology and invented the leap day.
Ptolemy did important work in mathematical geography, carrying on the tradition of Eudoxus, Aristotle, and Eratosthenes, and influenced geographic thought for the next fifteen centuries in this regard. He determined a method of finding longitude and latitude, and cataloged the longitude and latitude of some 8,000 places.
Astronomy advanced during that period with the work of Ptolemy but preceded by the Greek astronomers Heraclides, Aristarchus, and Hipparchus, and we should consider their work before that of Ptolemy.Heraclides, a fourth Century BC Greek, who was connected with both the Pythagorean and Platonic schools, is said to have been the first one to teach that the Earth turns on its own axis from West to East in twenty-four hours. He is said to have advanced the hypothesis that Mercury and Venus revolve about the Sun. He did not bring forth, however, any conception of the orbital or progressive motion of the Earth. Although he conceived of concentric spheres he could not explain why these planets were at times closer and other times farther from the Earth. It was during the Alexandrian period that epicycles, described previously, were contrived to explain irregularities in the motions of the planets.
Aristarchus of Samos (c 270 BC) met the objection that the motion of the Earth would cause changes in the apparent position of the stars by assuming that their distances were so great as to render the motion of the Earth a negligible factor. He is also said to have believed that the Earth moves around in an orbit besides rotating, a hypothesis quite daring at the time. The theory of epicycles mentioned previously came about because the Greek philosophers could not fathom the idea of motion in other than a straight line or a circle. Thus, the concept of an elliptical orbit for a planet would be incompatible with this philosophy. The theory at the time considered the Earth to be in the center of the universe and that the planets moved about in circular orbits around it. As it moved around in its orbit, a planet would also move in a second circular orbit with its center on the original orbit. The apparent retrograde motions of certain planets could be explained by this theory.
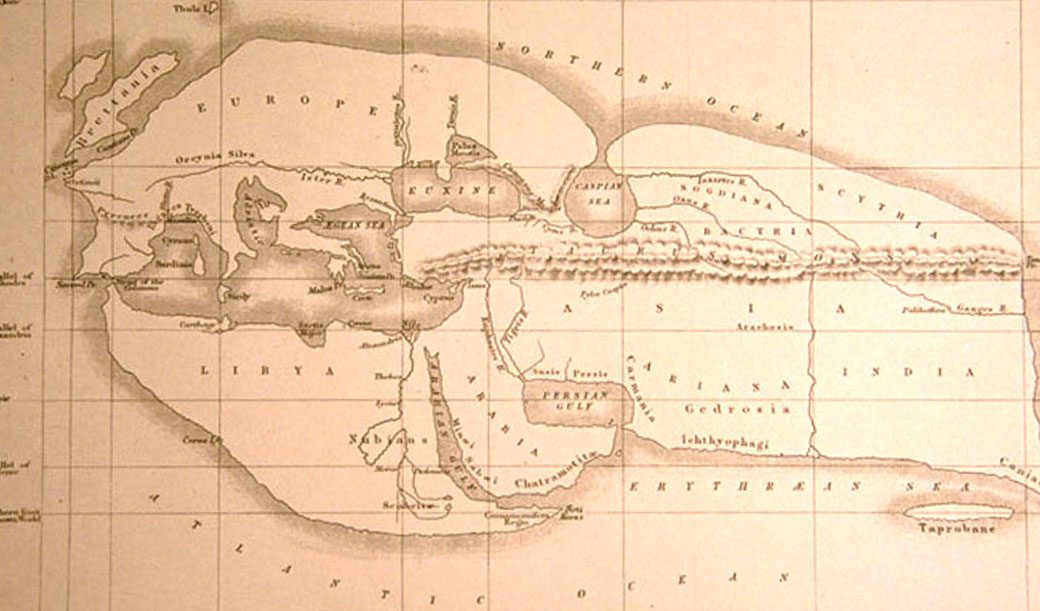 |
| 19th-century reconstruction of Eratosthenes’ map of the known world, c. 194 BC. via wikimedia commons |
The next great Greek astronomer was Hipparchus of Nicaea (c.190-c.120 BC), considered the founder of trigonometry, and considered by some the greatest astronomer in antiquity. He composed star catalogues, measuring the positions of stars and comparing these determinations with those made 150 years before. He thus discovered that the Earth’s axis itself rotates slowly and completes the cycle of rotation in thousands of years. This was concluded when he found changes, very slight in some cases, as much as two degrees in others, in the relative positions of stars mapped out during his time and in periods preceding. He determined the length of the year within six minutes, striving for greater accuracy and completeness of data. He made substantial improvements in the assessment of solar and lunar eclipses, and obtained a close approximation of the distance of the moon. He also laid the foundations of trigonometry by construction for astronomical use a table of chords, equivalent to the natural sine tables. He made very effective use of the records of early astronomers, critically considering their value, and worked out a consistent mathematical theory of the motions of the heavenly bodies so far as his data warranted.
These astronomers and mathematicians preceded Ptolemy and it was over 250 years after Hipparchus, in the second century AD, that Ptolemy further advanced the knowledge of astronomy. He lived in the city of Alexandria in the Roman province of Egypt, wrote in Greek, and held Roman citizenship. For Ptolemy, the Earth was still the center of the heavens and had no translatory motion. Discrepancies between observed and computed data, however, led Ptolemy to modify the Aristotelian concept that celestial bodies move in circular paths by assuming circles eccentric to that of the Earth. The line joining the centers of the circle and the Earth would revolve. His astronomical models were placed in convenient tables, useful for computing past or future positions of the planets.
Ptolemy’s treatise in astronomy is presented in the Almagest, the only surviving comprehensive ancient treatise on astronomy, perhaps the reason his name is more prominent than that of other ancient astronomers. The Almagest contains catalogues of stars and lists forty-eight constellations covering a limited area of the sky, using the work of Hipparchus in compiling the catalogues. The Almagest became the authoritative source for European astronomers over the next millennium. Ptolemy was also a geographer, providing a system for creating maps of the inhabited world. These maps characteristically covered the territory from the Atlantic Ocean (West) to the middle of China (East) and from the Shetland Islands (north) to the East coast of Africa (South). cf – Eratosthenes illustration above.
After Ptolemy, astronomy did not advance to any great extent for a millennium. In Ptolemy’s time, astronomers relied more on observation that the early Greek astronomers, basing their theories on observation, rather than the reverse as with earlier Greek astronomers. We find illustrations of genuine scientific caution, especially with Hipparchus, who, having tested the planetary theories then in vogue and discovering their insufficiency, patiently collected fresh material so that some future astronomer could arrive at an improved theory.
Aside from mathematics, astronomy, and geography, the Alexandrians were noted for their medical tradition. It was there that anatomy was first freely studied with the result that many of the grotesque errors of the earlier Greeks, including Aristotle, were corrected. Erasistratus (c.304-c.250 BC) founded a school of anatomy in Alexandria and undertook anatomical research. He opposed the Hippocratic theory of the four humors (blood, phlegm, black bile, and yellow bile) but instead favored the concept that Air, Fire Earth, and Water were the constituents of all things. He is called the father of experimental physiology. It is believed that the valves of the heart were first studied and named by him, as well as parts of the brain. He also concluded that the heart was a pump, not a center of sensations. He attributed the pulse to cardiac contraction although he believed that contraction of the portal vein to the liver also promoted blood flow, a concept believed by others at the time. He was one of the first to distinguish between arteries and veins. He still believed in an “animal spirit” (pneuma) with the arteries carrying it as part of the air. When an artery was severed, blood escaped and blood in the veins filled it due to the vacuum created. He also believed that this spirit was carried in the nerves. However, he did separate the function of sensory and motor nerves and associated them with the brain, providing a description of the cerebrum and cerebellum. Many of Erasistratus’s concepts were later accepted and popularized by Galen, who corrected and modified them based upon his later investigations.
Galen (c.129-2100/216 AD), born in Pergamum, became the most noted medical philosopher of the Alexandrian school (see II: Hippocrates v. Galen). In medieval Europe, Galen’s writings on anatomy became the mainstay of the medieval physician’s university curriculum. Galen bolstered Erasistratus’s concept of the functioning of the brain as responsible for controlling the function of muscles through nerves. His theory was based on nerve ligation studies.
Galen studied the splanchnic circulation and believed that partially digested food entered the portal vein circulation from the stomach, with venous flow aided by stomach compression and by attraction of the chyle to the liver. However, the portal blood ebbed and flowed, also carrying black bile to the spleen, and eventually to the stomach. In the liver, natural spirits were added to the blood which entered the heart which added “vital spirits”. Blood entering the brain received “animal spirits:” from the brain.
Galen saw himself as both a physician and a philosopher, as he wrote in his treatise entitled That the Best Physician is also a Philosopher. Galen was very interested in the debate between the rationalist and empiricist medical sects,and his use of direct observation, dissection, and vivisection represents a complex middle ground between the extremes of those two viewpoints. He was a teleologist, believing that function develops structure, and that the structure of an organ is the best possible one for its particular function. He also believed that there were causal relationships between the heavens and the human body. He was opposed to the atomists, who attempted to reduce physiology to physics, believing the body to be governed by a physis, or nature, the faculties of which it was the problem of physiology to deal. Some of Galen’s ideas were used by physicians in their practices up to the nineteenth century.
Around the third century AD Alexandrian influence began to decline. The Roman world was now completely encompassing the former Greek world in intellectual interests, and was in general alienated from mathematics and science. Geometry had reached a relatively complete development within the possible range of the Euclidean methodology. Algebra under Diophantus had reached a position that would not be attained again for centuries to come. Under Roman autocracy and Christian hostility, science and experimentation shrank in magnitude. Advances in science passed to the Arabs, who transmitted their advances back to the West at the end of the Medieval period. However, the contributions of the Greeks and Alexandrians influenced scientific systematology until, in the sixteenth and seventeenth centuries, modern science and scientific method began to emerge. There is some value, however, in discussing the approaches to scientific philosophy under the Romans.
References
- Fishman AP and Richards DW.Circulation of the Blood.Men and Ideas. American Physiological Society Bethesda MD 1982
- Artmann, Benno (1999). Euclid: The Creation of Mathematics. New York: Springer. ISBN 0-387-98423-2.
- Heath, Thomas L. (1981). A History of Greek Mathematics, 2 Vols. New York: Dover Publications. ISBN 0-486-24073-8 / ISBN 0-486-24074-6
- Heath, Thomas L. (1981). A History of Greek Mathematics, 2 Vols. New York: Dover Publications. ISBN 0-486-24073-8 / ISBN 0-486-24074-6
- Gow, Mary (2005). Archimedes: Mathematical Genius of the Ancient World. Enslow Publishers, Inc. ISBN 0-7660-2502-0.
- Hasan, Heather (2005). Archimedes: The Father of Mathematics. Rosen Central. ISBN 978-1-4042-0774-5
Pickover, Clifford A. (2008). Archimedes to Hawking: Laws of Science and the Great Minds Behind Them. Oxford University Press.ISBN 978-0-19-533611-5. - Toomer, G.J. (1970). “Apollonius of Perga”.Dictionary of Scientific Biography1. New York: Charles Scribner’s Sons. pp. 179–193. ISBN 0-684-10114-9.
- Boyer, Carl B. (1991).”Apollonius of Perga”. A History of Mathematics (Second ed.). John Wiley
- Vogel, Kurt (1970). “Diophantus of Alexandria”.Dictionary of Scientific Biography 4. New York: Scribner.& Sons, Inc. pp. 156–157. ISBN 0-471-54397-7
- Boyer, Carl B. (1991).”Revival and Decline of Greek Mathematics”. A History of Mathematics (Second ed.). John Wiley & Sons, Inc. p. 178.ISBN 0-471-54397-7
- Landels, J.G. (2000). Engineering in the ancient world (2nd ed.). Berkeley: University of California Press. ISBN 0-520-22782-4.
- Marie Boas, “Hero’s Pneumatica: A Study of Its Transmission and Influence”, Isis, Vol. 40, No. 1 (Feb., 1949)
- Alan C. Bowen, Robert B. Todd, Cleomedes’ Lectures on Astronomy. A Translation of The Heavens with an Introduction and Commentary. University of California Press, 2004.ISBN 0-520-23325-5
- Smith, A.M. (1996) Ptolemy’s theory of visual perception: An English translation of the Optics with introduction and commentary. Transactions of the American Philosophical Society, Vol. 86, Part 2. Philadelphia: The American Philosophical Society.
- Taub, Liba Chia (1993). Ptolemy’s Universe: The Natural Philosophical and Ethical Foundations of Ptolemy’s Astronomy. Chicago: Open Court Press. ISBN 0-8126-9229-2.
- Dorandi, Tiziano (2005), “Chronology”, in Algra, Keimpe; Barnes, Jonathon; Mansfeld, Jaap et al., The Cambridge History of Hellenistic Philosophy, Cambridge University Press, ISBN 0-521-61670-0
- Furley, David J.; Wilkie, J.S., eds. Galen on respiration and the arteries. Princeton, NJ: Princeton University Press. ISBN 0-691-08286-3.
- Lonie, I. M. (1964).”Erasistratus, the Erasistrateans, and Aristotle”. Bulletin of the History of Medicine 38: 426–443.
- Smith, W. D. (1982).”Erasistratus’s dietetic medicine”. Bulletin of the history of medicine 56 (3): 398–409. PMID 6753988.
- Porter, Roy, ed. (2000). “Heraklides of Ponticus”. The Hutchinson Dictionary of Scientific Biography (1st ed.). Hodder & Stoughton.ISBN 978-1859863046
- Hans B. Gottschalk (1980) Heraclides of Pontus, New York, Oxford University Press
- Stahl, William (1970). “Aristarchus of Samos”.Dictionary of Scientific Biography1. New York: Charles Scribner’s Sons. pp. 246–250. ISBN 0-684-10114-9
- Bowen A.C., Goldstein B.R. (1991). “Hipparchus’ Treatment of Early Greek Astronomy: The Case of Eudoxus and the Length of Daytime Author(s)”. Proceedings of the American Philosophical Society135(2): 233-254.
- Bowen A.C., Goldstein B.R. (1991). “Hipparchus’ Treatment of Early Greek Astronomy: The Case of Eudoxus and the Length of Daytime Author(s)”. Proceedings of the American Philosophical Society135(2): 233-254.
- C. Gill, T. Whitmarsh, and J. Wilkins (eds), Galen and the World of Knowledge (New York and Cambridge, 2009) (Greek Cultures in the Roman World).
- Galen (1991).On the therapeutic method. R.J. Hankinson, trans. Oxford: Clarendon Press. ISBN 0-19-824494-0.
- Galen (1991).On the therapeutic method. R.J. Hankinson, trans. Oxford: Clarendon Press. ISBN 0-19-824494-0.
PHILIP R. LIEBSON, MD, graduated from Columbia University and the State University of New York Downstate Medical Center. He received his cardiology training at Bellevue Hospital, New York and the New York Hospital Cornell Medical Center, where he also served as faculty for several years. A professor of medicine and preventive medicine, he has been on the faculty of Rush Medical College and Rush University Medical Center since 1972 and holds the McMullan-Eybel Chair of Excellence in Clinical Cardiology.

Leave a Reply