Philip Liebson
Chicago, Illinois, United States
 |
| Thales |
It was not until we reach the Greeks that we find science emerging as an autonomous activity. It is only then that the scientific spirit began to emerge. Thales of Miletus, one of the Ionian philosophers, is said to have set out to answer the question, “Of what and in what way is the world made?” Thales’s question reflects their passion of disinterested curiosity, a spirit necessary to science which had not been apparent in previous traditions. With the Greeks we first find and interest in knowledge for the sake of knowledge. The Greeks also seemed to be the first people with a thorough grasp of mathematical reasoning. With this tool, the Greeks felt that mathematics could provide the key to all knowledge. This was especially true of the Pythagoreans, who believed that everything, whether encompassing moral qualities or physical properties, was a manifestation of numbers. With deductive reasoning, they pursued their task of finding a mathematical order in the universe. However, with the Greeks as a whole, the patience of minute observation was not nearly so prominent. Thus, a complete scientific mentality had not yet been attained.
Greek science and civilization owed a great deal to the traditions of Egypt and Babylonia. The land-surveying formulae of the Egyptians, for instance, gave rise, in the hands of the Greeks, to deductive geometry. With the Egyptians, these formulae had been discovered for practical usage, not for theoretical knowledge. Rectangles of land of the same size were divided among the Egyptians and taxed accordingly. If the Nile happened to overflow, something which could be depended upon, the persons who lost any portion of their land would have proportionate abatement of taxes. Thus arose geometry, according to Herodotus. The Egyptians also developed fractions. A discussion of this aspect of mathematics is found in the Ahmes Papyrus, dating from sometime between 1700 and 2000 BC. There is found here, as well as in other manuscripts, the decomposition of fractions into fractions with unit numerators.
The Babylonians developed two number systems with bases ten and sixty. The base sixty has survived in time and geometric angle measurement. In the field of astronomy, the Babylonians identified five heavenly bodies as planets and computed the length of the year to 365 days. With the Babylonians we also find an interest in the study of eclipses. In connection with astronomical observations they invented a method for measuring time by means of a water clock.
With both Egyptian and Babylonian traditions, we find that mathematics is connected with religion and mysticism. This was especially apparent in Egypt, where religion was completely enmeshed in geometry. With the Greeks, mysticism and religion were divorced for the most part from mathematics, although we find mysticism prevalent in Pythagorean concepts of numbers. Thus, in studying the traditions before the Greeks, we find that the only scientific problems that interested their predecessors were those that had a direct bearing on practical affairs. They seem to have shown little curiosity in the workings of nature. Their discoveries were incorporated into their religions and philosophical schemes and were interested in accordance with their religious and philosophical principles.
 |
| Pythagoras |
The sense of curiosity and spirit of inquiry can first be found, as far as we know, in the minds of Ionian philosophers, who lived in the sixth and seventh centuries BC. Most notable of these philosophers was Thales (c.636-c.546 BC). With Thales we find for the first time a search for fundamental principles and their logical correlations. With Thales we also find the beginning of the road of Greek science, directed toward the general and the abstract. Thales traveled extensively and came into contact with Egyptian concepts, especially that of the priesthood. He occupied himself with the study of stars and geometry. He taught that the year has 365 days, that the equinoxes divide the year unequally, and that the moon is illuminated by the sun. Several geometrical theorems are attributed to him, such as the one stating that the base angles of an isosceles triangle are equal. Most of the facts ascribed to Thales may well have been known by the Egyptians, but for them those facts would have remained unrelated. For the Greeks there was already a characteristic tendency to generalize in an abstract way. Speculating on cosmology, Thales believed the Earth to be a circular disk floating in water. Water was considered by him to be the fundamental element from which everything generates and into which everything degenerates.
A second native of Miletus in Ionia was Anaximander (c. 611-545 BC). He had a different interpretation of nature, believing that all things were made from a substance with properties between those of air and water and that the Earth was the center if the universe, balanced in its center, because in such a position it would not tend to fall in one direction or another. This point of view shows the tendency of the Greek philosopher to emphasize geometrical symmetry. Among other things, he collected data from Ionian sailors and constructed a map of the earth, and, it is said, introduced the sun dial into Greece.
Anaximenes, a contemporary of these two philosophers, (c.585-525 BC) also an Ionian, believed the stars to be fixed in the celestial vault. For him, it was air that was the cause of all things, which were accordingly formed by the compression and rarefaction of the air, He believed that the heat of the sun is due to its rapid motion, but the stars are too remote to give out heat.
After the school of Thales, we come to the Pythagorean School of mathematics. It was with Pythagoras (c.570-495 BC) and his followers that we find the beginnings of the systematic foundations of the structure of mathematics. Pythagoras appears to have been influenced by the Egyptians while there. He founded a school in Southern Italy that had the character of a secret society. He appears to have interested himself in the theory of numbers, especially in connection with geometry and music. He is also said to have introduced weights and measures among the Greeks. Pythagoras classified mathematics into arithmetic, or absolute numbers, music, or applied numbers, geometry, or magnitudes at rest, and astronomy, or magnitudes in motion. This division continued in vogue for about 2000 years.
 |
| Pythagoreans Celebrate Sunrise by Fyodor Bronnikov |
The distinction between abstract and concrete arithmetic had been emphasized among the Greeks in comparatively early times. Arithmetic and geometry were distinguished from mechanics, optics, geometry, computation, surveying, and music. Pythagoras, in pure arithmetic, believed in an origin and beginning of all numbers, itself not a number, which was called “unity”. The Pythagoreans distinguished prime from composite numbers, and worked on complex algebraic theorems. Unknown and given quantities were employed by them although there was no algebraic symbolism as of yet. In geometry, the Pythagoreans formulated definitions of the fundamental elements, such as line and surface. They developed a fairly complete theory of the triangle, including the fundamental proof that the sum of the angles of the triangle is two right angles. The four elements – air, fire, earth, and water – were shown in symbolic correspondence by the appropriation of geometrical configurations. With the Pythagorean Theorem, we come to the interesting problem or irrationals. With the isosceles right triangle, for instance, it was found that if the length of two equal sides was 1 in each case, the length of the hypotenuse could only be expressed approximately, because the number was irrational. However, Pythagoras’s use of geometrical instead of algebraic proof side-stepped this problem. With Pythagoras we may recognize the characteristic elements of the inductive method, first, observation of the fact that in a 3-4-5 right triangle, the sum of the squares of the two sides is equal to that on the hypotenuse; secondly, the formulation of the hypothesis that this may be true for right triangles in general; thirdly, the verification of this for particular cases. Then, by deduction, the hypothesis is confirmed. With the Pythagoreans, the universe was believed to consist of four elements, to be a sphere with a spherical earth as center, and to have life.
 |
| Anaxagoras; part of a fresco in the portico of the National University of Athens |
Later Pythagoreans, especially Philolaus, about 400 BC, attributed the apparent motion of the heavenly bodies from East to West to the motion of the earth in the opposite direction. The earth was believed to revolve around a “central fire” (not the sun). This was not, therefore, a rotation. The Earth was closest to the central fire, then, in order, the moon, sun, Venus, Mercury, Mars, Jupiter, and Saturn. Hicetas, another Pythagorean, believed that nothing moved except the Earth, which rotates around its own axis.The activity of the Pythagoreans continued to be important until about 400 BC when the school of Plato and the Athenians began to come into prominence. The Pythagorean school had developed the idea of the universe governed by mathematical laws, had established induction and deduction as mathematical tools, and had moved in the direction of the use of logic, although there was still an element of mysticism, carried over, possibly, from Egyptian mathematics.
In the fifth century BC, the “Golden Age” of Greece, we find a rapid expansion of Greek science, especially mathematical science, which was less dependent upon externals than natural or physical sciences. In Plato and the Academy we find a definite trend toward the separation of science and philosophy.This is also especially pronounced in the medical works of Hippocrates. During this period, also, the atomists come into prominence,
Anaxagoras (c. 500-c.428 BC) paved the way for atomism with his theory of nature and the origin of the cosmos. He believed that the cosmos had been formed by the combination and differentiation of primitive elementary substances, or seeds of matter. In addition to this, he undertook the problem of squaring the circle. He explained the moon’s phases correctly, also depicting solar and lunar eclipses, and he correctly believed that the Earth’s axis is inclined. However, it was his atomic theory of nature that was most influential.
Leucippus and Democritus carried further the theory of atomism. They believed that nature consists of two fundamental components, atoms and void. Atoms come in an infinite variety of shapes and sizes, each indestructible, immutable, and surrounded by a void where they collide with the others or hook together to form a cluster. Clusters of different shapes, arrangements, and positions give rise to the various macroscopic substances in the world. Their contribution of skepticism renders a greater service than their positive contributions to science, which were neither important nor novel. Leucippus believed that atoms were indivisible and infinite in number, with only quantitative differences among them. He also saw space as being infinite in magnitude. Democritus, more famed than Leucippus, held closely to the latter’s interpretation of the cosmos.
The sophists also came into prominence in the fifth century BC. They denied the possibility of objective and universal truth, truth being relative and subjective. Their function was to instruct their pupils in the method of achieving worldly success. Science was not generally cultivated as a leading subject, but mathematics was esteemed as a means of discipline, and several of the sophists made notable contributions to its development. Hippias of Elis, the first sophist of importance, invented a curve called the quadratrix which served for the solution of two of the three celebrated problems of Greek geometry: the quadrature of the circle and the trisection of an angle.
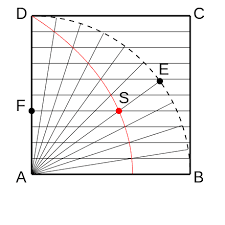 |
| Quadratrix (red); snapshot of E and F having completed 60% of their motions |
Before then, the problem could not be solved by any elementary means of geometrical construction. It was eventually found impossible to solve the three problems geometrically. Two of the sophists, however, mad an interesting contribution to the problem of squaring the circle, by means of inscribed and circumscribed polygons. These sophists, Antiphon and Bryson, repeatedly doubled the number of sides until the polygon became more nearly equivalent to the circle. Bryson employed both inscribed and circumscribed polygons, doubled their sides, and stated that the area of a circle may be considered an arithmetic mean between them.
Hippocrates of Chios (c.470-410 BC) (the mathematician, not the physician) is said to have been the first to make use of the reduction ad absurdum as a method of relating one proposition to another. Hippocrates worked on lunes, or areas bounded by circles, to allow him to figure out the Greek geometrical problem of the squaring of the circle. With lunes, he attempts to form a connection between rectilinear and curvilinear figures, and is quite successful in this respect.
Zeno of Elea (ca. 490–430 BC) represents an important phase of philosophical criticism of mathematics, with his paradoxes. These paradoxes show that an analysis of motion leads to absurdity. With two of his four paradoxes, he shows absolute motion to be impossible, and with the other two, shows relative motion to be impossible. Greek mathematicians criticized Zeno on his use of “infinitesimals”, or exceedingly small magnitudes, in his paradoxes. This is especially true in his Stadium paradox, where he “proves” the impossibility of relative motion showing that if it were so, one infinitesimal would equal two infinitesimals. The example is that of Achilles in a race with a tortoise. Whenever Achilles reaches some point the tortoise has been, he still has farther to go. Therefore, because there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise. Greek mathematicians were generally cautious about the use of infinitesimals for the most part, however, and it is only when we come to Archimedes that we find the notion of infinitesimals as means to discovery of solutions to problems. Zeno tried to reduce atomism to absurdity. Parenthetically, many of the paradoxes were resolved with the later invention of the calculus.
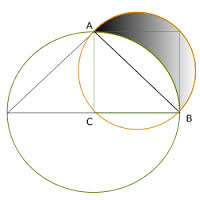 |
| The Lune of Hippocrates.Partial solution of the “Squaring the circle” task, suggested by Hippocrates. The area of the shaded figure is equal to the area of the triangle ABC. |
With Plato (c.428-348 BC) and the Academy, philosophy almost parts company with science. Before Plato, philosophy was almost wholly devoted to inquiries or speculations covering the universe and was substantially “natural;” philosophy. With Plato and since his time, the larger part of philosophy has been devoted to observation and speculation about the human mind, and has accordingly been called “moral” philosophy. Under Plato’s influence, mathematics first acquired its unified significance, as distinguished from geometry. Accurate definitions were formulated, questions of impossibility considered, methods of proof criticized and systematized, logical rigor insisted upon. The analytical method was developed, connecting that which is to be proven with that which is already known. Another influence is to isolate the problem by removing non-essential elements, and a third consists in proving that an assumption inconsistent with that which is to be proven is impossible. Thus, if X contradicts Y, X is false if Y has already been proven to be true. The synthetic method proceeds from the known to the unknown, and is completely valid for the Greeks. The Greek mathematicians would thus analyze the axioms from the theorems after the theorems had themselves been synthesized from axioms which were assumed to be true.
In the sphere of cosmology, Plato believed the Earth to be at the center if the universe, with the heavenly bodies being proportional to numbers of arithmetic and geometric progressions. Plato moved away from empiricismcompletely with hisTheory of Ideas, but did attempt to explain the natural universe by observation of the fourelements. At this time, it was generally believed that the Earth was a sphere.
Plato’s followers continued his development of mathematics with their rigorous study of problems. Geometry, with emphasis on philosophy, predominated over the theory of numbers, and studies of classic geometric problems led to the introduction of new curves and the study of conic sections by Menaechmus.
It is Eudoxus of Cnidus (408-355 BC) that we get important advances in mathematics and more especially, cosmology. A student of Plato, he was considered to be the greatest of classical Greek mathematicians, and in all antiquity second only to Archimedes. He developed the theory of proportion in mathematics to a great extent. Eudoxus reflected the general feeling of mathematicians of this period against bring infinitesimals into mathematical problems. He rigorously developed a precursor to the integral calculus which was also used by Archimedes in the following century. In applying the method, Eudoxus proved such mathematical statements as: areas of circles are to one another as the squares of their radii, volumes of spheres are to one another as the cubes of their radii, the volume of a pyramid is one-third the volume of a prism with the same base and altitude, and the volume of a cone is one-third that of the corresponding cylinder. Eudoxus introduced the idea of non-quantified mathematical magnitude to describe and work with continuous geometrical entities such as lines, angles, areas and volumes, thereby avoiding the use of irrational numbers. In doing so, he reversed a Pythagorean emphasis on number and arithmetic, focusing instead on geometrical concepts as the basis of rigorous mathematics.
 |
| The five elements, a thread through Greek philosophy, were expounded in Timaeus, his dialogue speculating on the nature of the physical world and human beings in which Plato claimed that the minute particle of each element had a special geometric shape: tetrahedron (fire), octahedron (air), ichoshedron (water), and cube (earth) |
At this time the irregularities of planetary motions were beginning to attract attention, and Eudoxus explained the irregularities as being caused by spheres moving in spheres. Thus the moon is carried on the equator if a sphere revolving from west to east in 27 days. The poles of this sphere are carried on a second sphere, which turns about the axis of the zodiac in 18 1/2 years. This concept was use to explain irregular motion to some extent although with certain planets the theory was inadequate. However, this is important as the first serious attempt to deal with the irregular motion of the planets. Eudoxus went beyond mere philosophical reasoning about the construction of the universe. He tried to systematically account for the planetary motions. His fame is also due to the introduction of the astronomical globe.
Aristotle (384-322 BC) is important in the context of scientific philosophy mainly for his contributions to methodology, although he made some notable contributions to mechanics, mathematics and astronomy. Conceptually, he believed that all events are known by demonstration. Demonstration rests on basic truths which are different in different sciences. The basic truths would be those elements in science in which the existence could not be proven, thus axiomatic. Science analyzes change, such as the causes of motion to distinguish among causes of change. The object of science is therefore changing subject matter, and the attempt to grasp the changeless truths from the changing subject matter. This is basically Aristotle’s philosophy of science. In the field of mechanics, he was convinced that the speed of falling bodies was proportional to their weight. He also believed that bodies moving in large circles moved faster than bodies moving in small circles. It was these two concepts that were applied either by himself or a disciple to formulate the principle of the lever and the balance.
It is at this time that we get the beginnings of rational medicine with the works of Hippocrates of Cos (c 460-c370 BC). Before the middle of the fifth century BC, there was essentially no scientific aspect of medicine. It was enmeshed in religion and was considered a priestly rather than a scientific profession. Alcmaeonid, in the sixth century BC, is probably the best known of the pre-Hippocratic physicians. He proved that the sperm does not originate, as was formerly believed, in the spinal marrow, and that the brain is the organ of the mind. He believed in a harmony of substances composing the human body, which was equivalent to health.
Separating medicine from religion, Hippocrates first urged that disease was a natural rather than a supernatural phenomenon. He believed in patient observation and also stressed that the physician should study the environment of the patient. He was a firm believer in prognosis instead of localized diagnosis, in other words, treating the body as a whole instead of evaluating and treating one part of the body that is diseased. He developed the humoral theory of pathology, whereby the individual is in good health when the four “humors” were in harmony. When there was an excess of one, disease occurred because of this “dyscrasia”, or disharmony. Thus we see here some Pythagorean philosophy, although Hippocrates was firm in the belief that philosophy should be divorced from medicine. Hippocrates’s works later became dogmatized by his followers, who, feeling that Hippocrates had completely covered empirical medicine, stressed deduction from these observations. They were essentially logicians, and thus put medicine on a more theoretical plane, which was completely contradictory to the thoughts of Hippocrates. However, the basic structure of Hippocratic thought itself was continuousuntil the time of Galen (AD 129 -c201/216).
After Hippocrates, the medical tradition continues with Theophrastus (372-287 BC), a pupil of Aristotle, and head of the Academy. He was an early student of plants. He wrote large works including On the History of Plants, and On the Causes of Plants. In these, 500 species of plants are described, chiefly with reference to their medicinal uses. Theophrastus differs from Aristotle in his de-emphasis of purpose and final cause. The works of Theophrastus eventually became one of the chief sources of the later herbals, or collections of plant descriptions put together for medicinal purposes.
Theophrastus was preceded by Diocles (c. 400-301 BC) (not to be confused with Diocles the mathematician in the third century BC), who was presumably the author of the first Greek herbal. He sought causes for diseases, and relied on the harmony of the body and soul. His work is said to have influenced Aristotle in his study of biology.
Besides the Hippocratic tradition, derived in some part from the tradition of Cos, his birthplace, there was also the Cnidean tradition, which ran parallel to that of Cos. This tradition concentrated on diagnosis and anatomical studies. Eristratus (310-250 BC), a proponent of that school, completely denied the humoral theory and stressed diagnosis.
At about 330 BC, with the subjugation of Greece by Alexander, the further development of Greek civilization on its own soil was checked. It is here that one tradition ends, if we may say that a tradition ends at a fixed point in time and another begins. For now we move from speculative science, characteristic of the Greeks in the golden Age, to the empirical science characteristic of the Alexandrians. Here begins the age of the specialist. Why was there such a change in traditions? Perhaps it was because the speculation in Greek scientific philosophy had advanced too rapidly in a theoretical plane for the material world around it. Perhaps, also, it was due to a blending of cultures in a center which was for a time the crossroads of civilization. The legacy of the Greek tradition is the spirit of theoretical inquiry that brought about the beginnings of scientific structure. It was for the Alexandrians to fill up this framework with observation and experimentation of such intensity that never had been seen before.
References
- Berryman, Sylvia, “Ancient Atomism”, The Stanford Encyclopedia of Philosophy (Fall 2008 Edition), Edward N. Zalta (ed.), http://plato.stanford.edu/archives/fall2008/entries/atomism-ancient/
- The atomists, Leucippus and Democritus: fragments, a text and translation with a commentary by C.C.W. Taylor, University of Toronto Press Incorporated 1999, ISBN 0-8020-4390-9, pp. 157-158.
- Couprie, Dirk L. (2011). Heaven and Earth in Ancient Greek Cosmology: from Thales to HeraclidesPonticus. Springer.ISBN9781441981158.
- Luchte, James (2011). Early Greek Thought: Before the Dawn. London: Bloomsbury Publishing. ISBN978-0567353313.
- O’Grady, Patricia F. (2002). Thales of Miletus: The Beginnings of Western Science and Philosophy. Western Philosophy Series 58.Ashgate.ISBN9780754605331
- Kirk and Raven, ThePresocratic Philosophers, Second Edition (Cambridge University Press, 1983)
- Kirk, G.S., J.E. Raven, and M. Schofield.”Anaximenes of Miletus.”The Presocratic Philosophers. Cambridge: Cambridge University Press, 1984.
- Guthrie, W.K.C. “The Milesians: Anaximenes.” A History of Greek Philosophy. Cambridge: Cambridge University Press, 1962.
- Burkert, Walter (1972). “Lore and Science in Ancient Pythagoreanism”.Harvard University Press.
- O’Meara, Dominic J. Pythagoras Revived. Oxford University Press, 1989.ISBN 0-19-823913-0
- Guthrie, W. K. A History of Greek Philosophy: Earlier Presocratics and the Pythagoreans, Cambridge University Press, 1979. ISBN 0-521-29420-7
- Anaxagoras of Clazomenae: Fragments and Testimonia : a text and translation with notes and essays. University of Toronto Press. 2007
- Bakalis, Nikolaos (2005). Handbook of Greek Philosophy: From Thales to the Stoics: Analysis and Fragments, Trafford Publishing, ISBN 1-4120-4843-5.
- Cartledge, Paul, 1997, Democritus (The Great Philosophers), London: Routledge.
- Furley, David J., 1987, The Greek Cosmologists vol 1: The Formation of the Atomic Theory and its Earliest Critics, Cambridge: Cambridge University Press.
- Pendrick, G.J., 2002, Antiphon the Sophist: The Fragments, Cambridge: Cambridge University Press.Cambridge UP, 1989.
- Heath, Thomas (1981). A History of Greek Mathematics, Volume I: From Thales to Euclid. Dover Publications, Inc. ISBN0-486-24073-8.
- A R Amir-Moéz and J D Hamilton, Hippocrates, Recreational Math.7 (2) (1974), 105-107.
- Morris Kline, Mathematical Thought from Ancient to Modern Times Oxford University Press, 1972
- McEvans, James (1998). The History and Practice of Ancient Astronomy.Oxford University Press.ISBN0-19-509539-1
- Heidel, William Arthur (1941), Hippocratic Medicine: Its Spirit and Method, New York: Columbia University Press
- Barnes, Jonathan (1995). “Life and Work”.The Cambridge Companion to Aristotle. Cambridge University Press..ISBN978-0-521-42294-9.
- Taylor, Alfred E. (1928). A commentary on Plato’s Timaeus. Oxford: Clarendon
- Grene, Marjorie; Depew, David (2004). The philosophy of biology: an episodic history. Cambridge University Press.ISBN978-0-521-64380-1.
- Smith, W. D. (1982).”Erasistratus’s dietetic medicine”. Bulletin of the history of medicine 56 (3): 398–409. PMID6753988.
PHILIP R. LIEBSON, MD, graduated from Columbia University and the State University of New York Downstate Medical Center. He received his cardiology training at Bellevue Hospital, New York and the New York Hospital Cornell Medical Center, where he also served as faculty for several years. A professor of medicine and preventive medicine, he has been on the faculty of Rush Medical College and Rush University Medical Center since 1972 and holds the McMullan-Eybel Chair of Excellence in Clinical Cardiology.

Leave a Reply